広告効果定量化のためのMMM(広告会社様/広告ご担当者様向け)リリース

株式会社Crosstabは表題のサービスを開始しました。詳細は以下をご参照願います。
今後も広告会社様/及び事業会社様のご担当者様に向けての情報をアップデートしていく予定です。

背景

広告チャネルは多様であるためその運用において、どこにどれだけの資本を投下するのかという意思決定は重要です。一方でそれらは属人的な経験による所や、事前事後のアンケート調査やGRP値などを参考に決定している事が多いです。しかしこの方法ではいくつか問題があります。まず①担当者の経験に左右されるためノウハウの固定化が困難である②アンケート調査では偏りが大きいまた定期的な調査が必要なる③GRPは延べリーチユーザ数であり実際にセールスに繋がったかは不明などが挙げられます。このような問題点を抱えながら依然として上記方法が用いられる理由は適切な代替方法すなわち、広告効果の厳密な算定を元に予算最適を行う仕組みが確立されていないからではないかと考えます。

目的

本ソリューションの目的はMarketing Mix Modeling(MMM)という手法を用い広告効果の定量化を行うための分析及びデータ収集を行い、貴社にとっての広告効果定量化モデルを作成し広告アロケーションの最適解を導きます。そして継続的にそれを用いた広告運用を行いマーケティングROIの最大化を目指します。

本ソリューションのイメージ

本ソリューションで得られるベネフィット

本ソリューション特徴

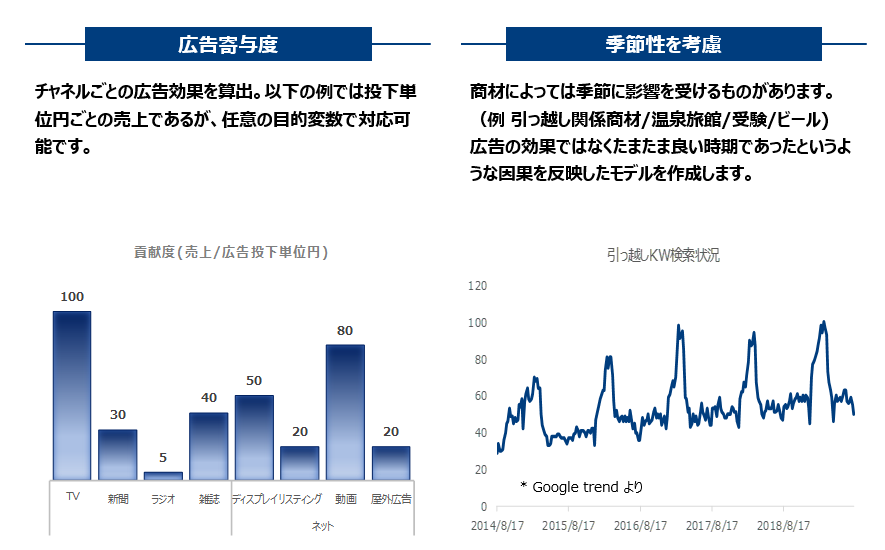
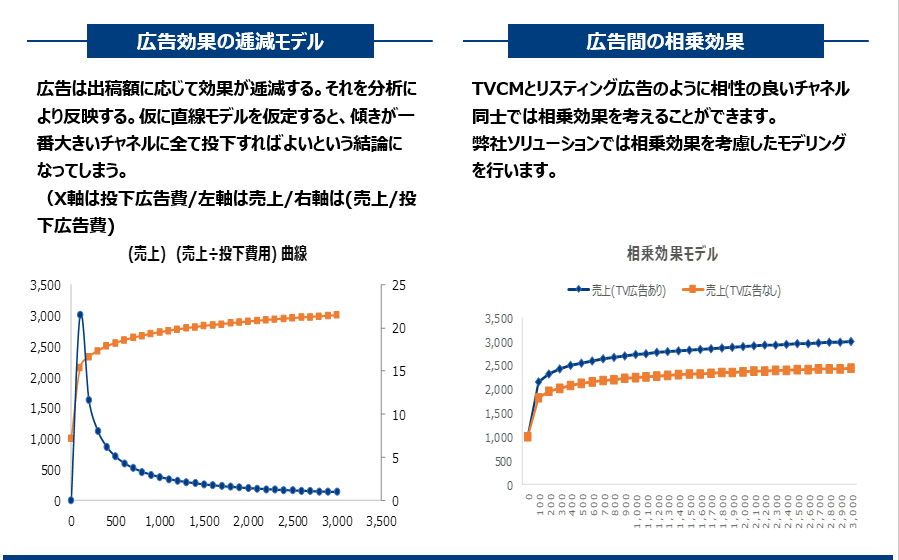
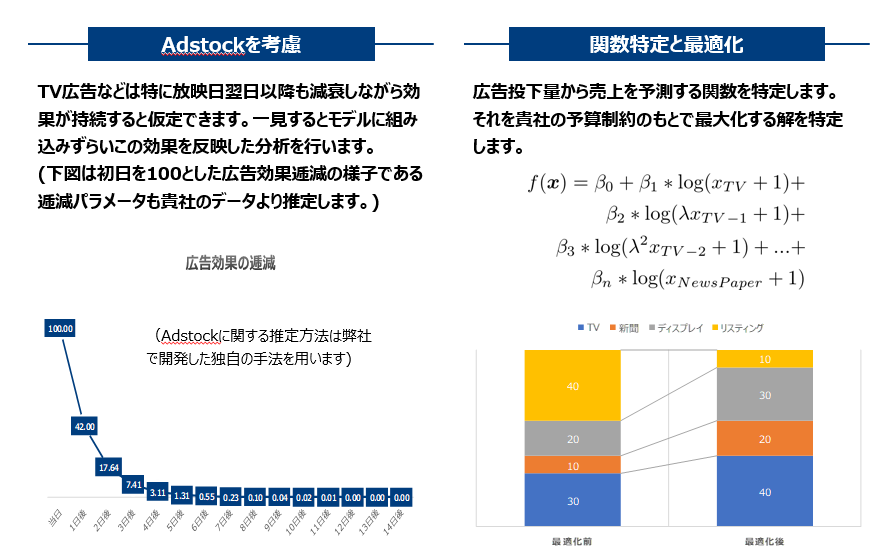
Marketing Mix Modeling の実行スキーム

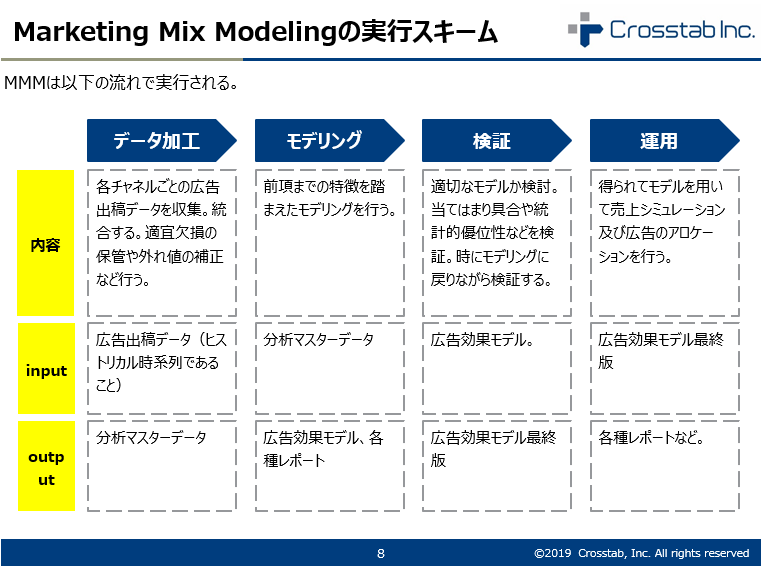
お客様でご準備頂くデータ

広告投下データ

• チャネルごとの広告投下費用の時系列データをご用意いただきます。費用ではなく費用に比例するGRPのようなものでも構いません。
• 時系列は日次データであることが望ましいです。期間は1年以上が望ましいです。

広告の成果指標データ

• 売上金額や個数及び検索数などの広告の目的に応じた成果変数のデータをご用意頂きます。
• 時系列は日次データであることが望ましいです。期間は1年以上が望ましいです。広告投下データと同じ期間であることが必要です。

（補足） ファイルは複数であって結構です。まとまっている必要はございません。

スケジュール

価格感

エンジン部分の稼働のみ（前項の#2)ご提供するプランAと全行程の支援を行うプランBからご案内しております。主に前者は広告代理店様及びコンサルティングファーム様などクライアント様に提供する事業者様向けで、後者さらに加えて事業会社様向けのプランです。

お問い合わせ

本ソリューションに関してのお問い合わせは https://crosstab.co.jp/contact-us/ よりお願い申し上げます。